写一写算法学习的记录,从易到难的都有,不间断更新。
易
1. 两数之和
给定一个整数数组 nums 和一个目标值 target,请你在该数组中找出和为目标值的那 两个 整数,并返回他们的数组下标。
你可以假设每种输入只会对应一个答案。但是,你不能重复利用这个数组中同样的元素。
示例:
给定 nums = [2, 7, 11, 15], target = 9
因为 nums[0] + nums[1] = 2 + 7 = 9
所以返回 [0, 1]
看到题目,其实马上能想到对应的算法,但是不是最优的。就是两遍for循环,取出元素相加判断是否是目标值,但是这种算法的时间复杂度很高,为O(n^2)。
iOS中可以使用集合来做,集合实际上是运用了哈希表的原理,哈希表查找元素的复杂度近似为O(1),这样我们可以用一层循环来完成。
在循环过程中,通过目标值减当前循环获得的元素值,获得需要的另一个元素值,然后拿这个元素值去集合中查找是否有对应值,如果有说明已经找到,如果没有则将当前循环到的元素插入集合。
func twoSum(_ nums: [Int], _ target: Int) -> [Int] {
var collect = Set<Int>.init()
var result = [Int].init()
for (index, value) in nums.enumerated(){
let needValue = target - value
if collect.contains(needValue){
result.append(nums.firstIndex(of: needValue)!)
result.append(index)
break
}
collect.insert(value)
}
return result
}
时间复杂度:只对数组循环了一次,集合的时间复杂度为O(1),所以最终的时间复杂度为O(n)。
空间复杂度:这里主要由集合中的元素个数决定,所以空间复杂度为O(n)。
中
1. 两数相加
题目:给出两个 非空 的链表用来表示两个非负的整数。其中,它们各自的位数是按照 逆序 的方式存储的,并且它们的每个节点只能存储 一位 数字。
如果,我们将这两个数相加起来,则会返回一个新的链表来表示它们的和。
您可以假设除了数字 0 之外,这两个数都不会以 0 开头。
实例:
输入:(2 -> 4 -> 3) + (5 -> 6 -> 4)
输出:7 -> 0 -> 8
原因:342 + 465 = 807
根据题意可以看出需要同时从头节点开始遍历两个单链表的每个节点,然后每个节点的值相加,和值作为新链表的一个节点,如果发生了进位,进位的数保存至下一次遍历用来计算,新链表节点只存储个位数。直接上图:
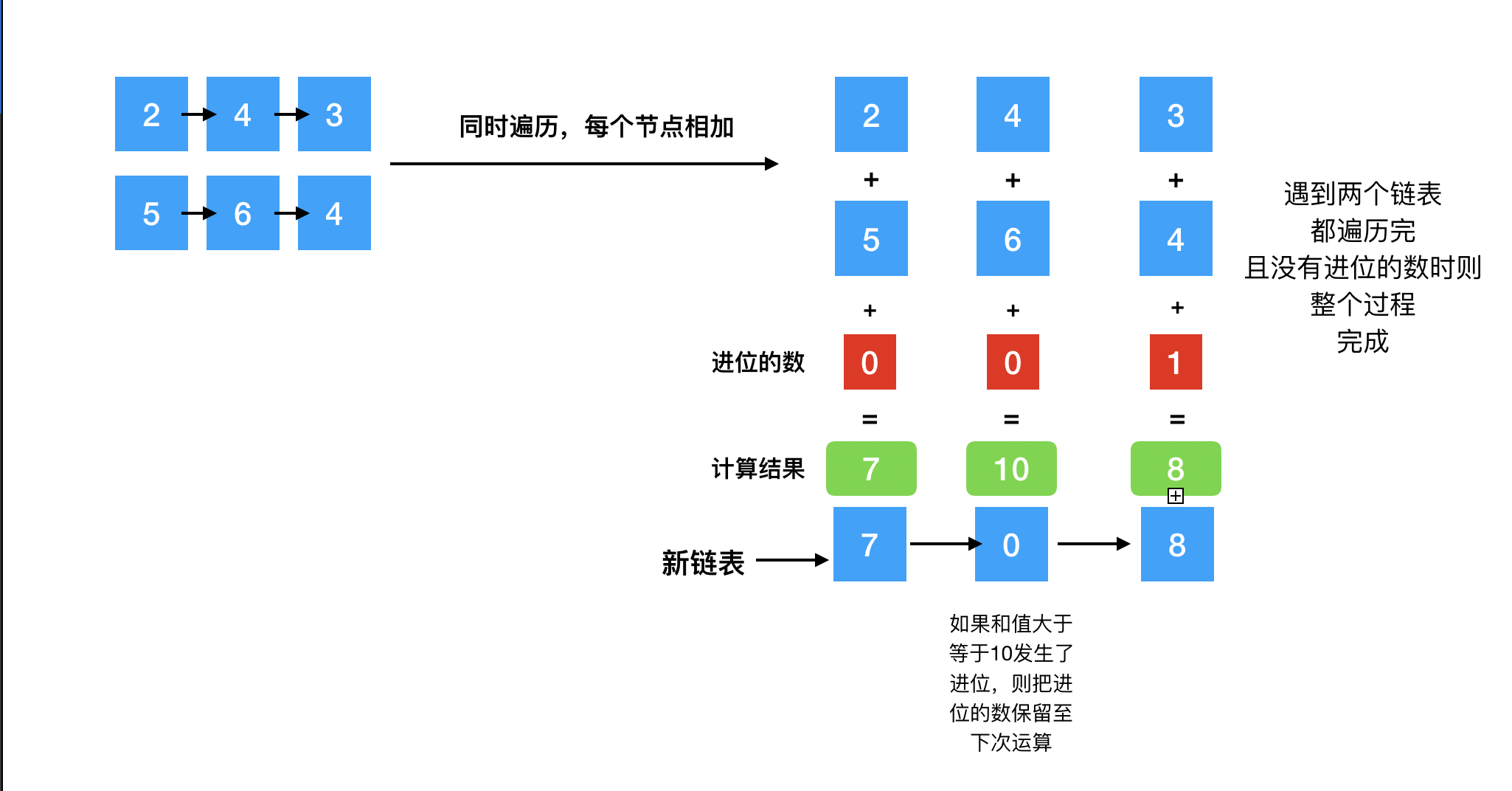
代码:
1 | public class ListNode { |
时间复杂度:根据上面代码,一次遍历,并且遍历的次数主要和两个链表最长的那个有关,所以时间复杂度为O(max(m,n));
空间复杂度:创建了一个新的链表作为结果返回,新链表的长度和输入的两个链表最长的那个有关,所以空间复杂度也为O(max(m,n)).
2. 无重复字符的最长子串
给定一个字符串,请你找出其中不含有重复字符的 最长子串 的长度。
示例 1:
输入: "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
示例 2:
输入: "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。
这个题目可以根据一个叫滑动窗口的方法来解决,如图:
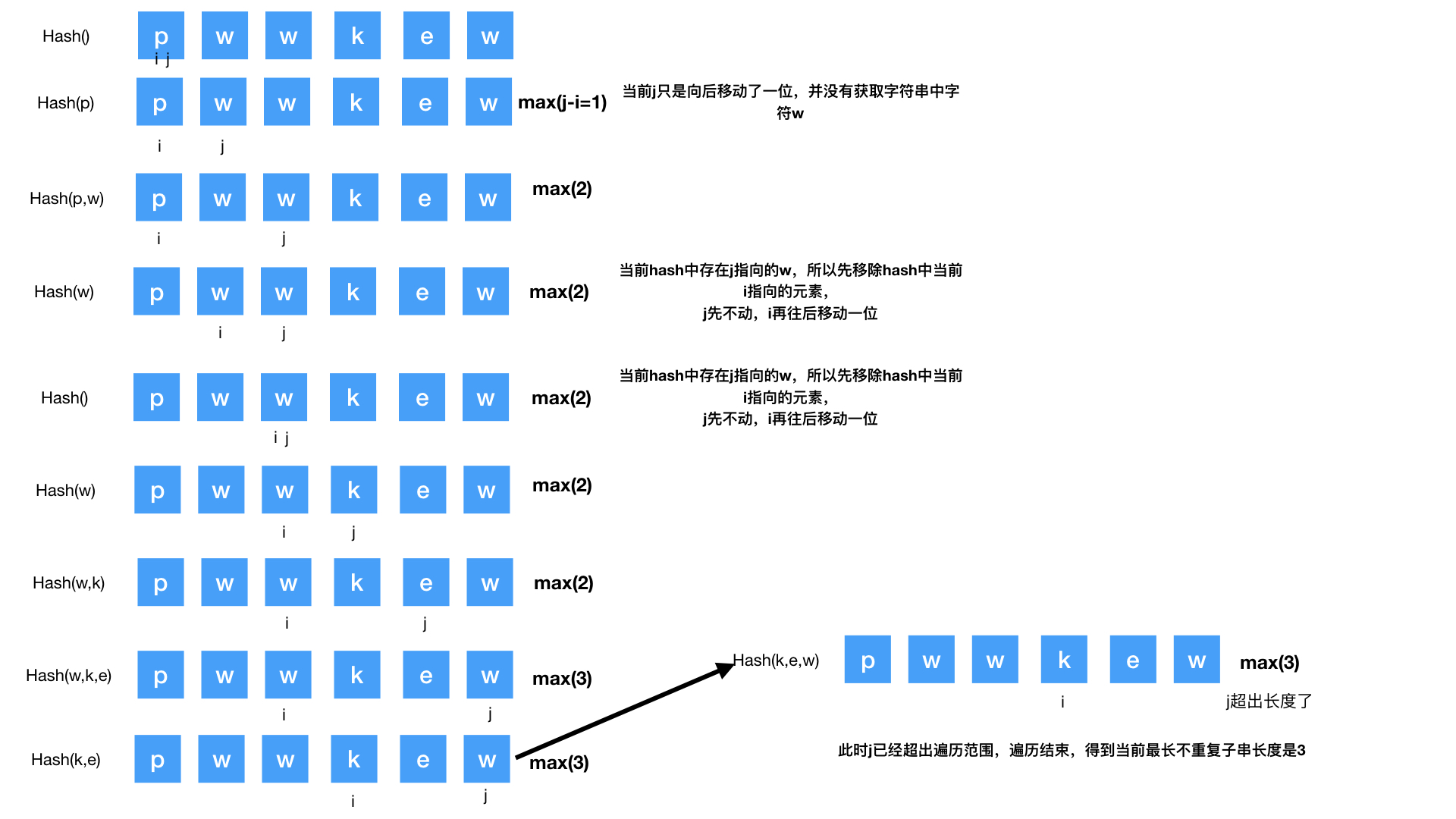
利用 i 和 j 两个索引从前往后遍历,用一个hash保存字符。首先 j 开始移动,i 不动,遇到 hash 中没有的字符就保存起来,如果hash的长度当前是最大的记录该长度; 如果 j 指向的值 hash 中已经存在,先移除掉 hash 中当前 i 指向的元素值,j 不移动,i 往后移动一位,以此类推,直到 i 或者 j 超出字符串长度,停止遍历,此时返回记录的最大的hash的长度。
代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32func lengthOfLongestSubstring(_ s: String) -> Int {
let characters = Array.init(s)
let len = characters.count
var i = 0
var j = 0
var maxValue = 0
var hashSet = Set<Character>.init()
while i < len && j < len {
if !hashSet.contains(characters[j]) {
hashSet.insert(characters[j])
j += 1
maxValue = max(maxValue, hashSet.count)
}else{
hashSet.remove(characters[i])
i += 1
}
}
return maxValue
}
}
时间复杂度:根据分析,用了 i 和 j 两个索引从前往后移动,总共移动了 2n 次,时间复杂度为 O(n);
空间复杂度:用了一个 hash 存储 字符,用了一个数组存储字符串 空间复杂度 O(n + m),m为hash的大小。